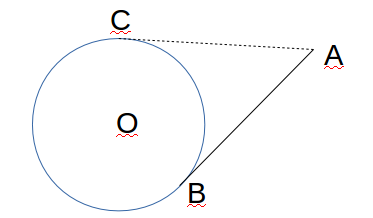
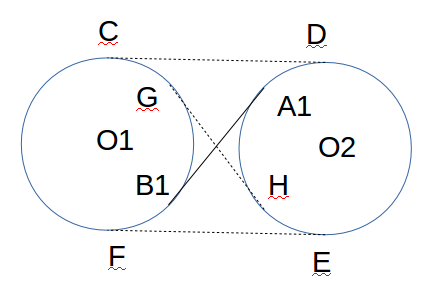
Може комусь треба буде:
(реалізація на Python)
[code=python]
import math
def get_intersection_of_circle(x0, y0, r0, x1, y1, r1):
# http://paulbourke.net/geometry/circlesphere/
# http://paulbourke.net/geometry/circlesphere/tvoght.c
dx = x1 - x0
dy = y1 - y0
d = math.sqrt(dx ** 2 + dy ** 2)
if d > r0 + r1:
raise Exception("No solution! Circles do not intersect!")
if d < abs(r0 - r1):
raise Exception("No solution! One circle is contained in the other!")
a = (r0 ** 2 - r1 ** 2 + d ** 2) / (2 * d)
x2 = x0 + (dx * a / d)
y2 = y0 + (dy * a / d)
h = math.sqrt(r0 ** 2 - a ** 2)
rx = - dy * (h / d)
ry = dx * (h / d)
return (x2 - rx, y2 - ry), (x2 + rx, y2 + ry)
def get_line_coefficients(x0, y0, x1, y1):
b = (y1 - y0) / (x1 - x0)
a = y0 - b * x0
return a, b # y(x) = a + b * x
def get_tangent_lines_to_one_circle(x0, y0, r0, x1, y1):
# https://goo.gl/1fAzhc
if np.isclose(x0, x1):
raise Exception("Don't work for x0 = x1!")
a, b = get_line_coefficients(x0, y0, x1, y1)
middle_x = (x0 + x1) / 2
return get_intersection_of_circle(x0, y0, r0,
middle_x,
a + b * middle_x,
math.sqrt((x0 - x1) ** 2 + (y0 - y1) ** 2) / 2)
def get_inner_tangent_lines_to_two_circle(x0, y0, r0, x1, y1, r1):
points = get_tangent_lines_to_one_circle(x0, y0, r0 + r1, x1, y1)
result = []
for point in points:
a2, b2 = get_line_coefficients(*point, x0, y0)
x2 = point[0] + (x0 - point[0]) * (r1 / (r0 + r1))
y2 = a2 + b2 * x2
x3 = x1 + (x2 - point[0])
y3 = y1 + (y2 - point[1])
result.append(((x2, y2), (x3, y3)))
return result
[/code]