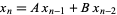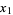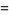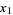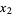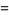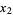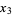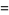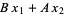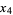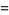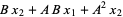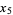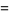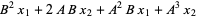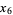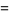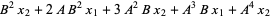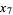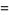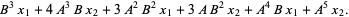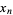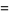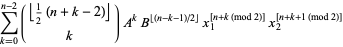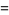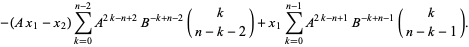Наведу 20 елементів послідовності:
3 4 -4 -24 -32 32 192 256 -256 -1536 -2048 2048 12288 16384 -16384 -98304 -131072 131072 786432 1048576
▼розрахунки
def an(n):
if n==1:
return 3
if n==2:
return 4
return 2*an(n-1)-4*an(n-2)
for i in range(1,21):
print(an(i),end=' ')
Що я тут бачу? По множниках:
3 4 (-1)*4 (-1)*2*3*4 (-1)*2*4^2 2*4^2 3*4^3 4^4 (-1)*4^4 (-1)*2*3*4^4 (-1)*4^5 4^5 і поки досить.
-1 повторюється в кожній другій трійці, починаючи з 3-го елемента. Прибираємо, щоб далі не заважала:
3 4 4 2*3*4 2*4^2 2*4^2 3*4^3 4^4 4^4 2*3*4^4 2*4^5 2*4^5
3 повторюється в кожному 3-му елементі, починаючи з 1-го. Прибираємо і переводимо в степені 2:
1 2^2 2^2 2^3 2^5 2^5 2^6 2^8 2^8 2^9 2^11 2^11
Степені:
0 2 2 3 5 5 6 8 8 9 11 11.
Це майже лінійна формула, тільки кожен 3-й елемент, починаючи з 2-го, більший на 1.
Ніби все. Тепер клепаємо формулу. Зараз голова не варить, тому буду робити це брудно, нехорошими функціями. Ліньки думати, чи можна хорошими.
(-1)^[n/3], де [] - ціла частина числа, буде давати 1 при 1,2,6,7,8,12... і -1 при решті.
3-2*sign((n-1) mod 3), де sign - знак (1 для додатних, -1 для від'ємних, 0 для нуля), mod - остача від ділення буде давати 3 при n=1,4,7,... і 1 при решті.
n-sign((n+1) mod 3) буде давати послідовність 0, 2, 2...
Отже,
f(n)=(-1)^[n/3]*(3-2*sign((n-1) mod 3))*2^(n-sign((n+1) mod 3))
виглядає доволі схожим на шукану формулу. Спробуємо довести, що це вона. База індукції:
f(1)=(-1)^[1/3]*(3-2*sign((1-1) mod 3))*2^(1-sign((1+1) mod 3))=
=(-1)^0 * (3-2*sign(0))*2^(1-sign(2))=3*2^0=3
f(2)=(-1)^[2/3]*(3-2*sign((2-1) mod 3))*2^(2-sign((2+1) mod 3))=
=(-1)^0 * (3-2*sign(1))*2^(2-sign(0))=2^2=4
Перехід: довести, що
f(n)=2f(n-1)-4f(n-2)
Спробуйте зробити це самостійно, але я б дав 90%, що це вдасться розглядом 3 випадків: n=3l, n=3l+1 і n=3l+2.