Re: Шлях на математичну вершину
Ой яка краса!
1) А чим таке анімують?
2) А чи можна ще подивитися, як вектори «дихають»?
Ви не увійшли. Будь ласка, увійдіть або зареєструйтесь.
Ласкаво просимо вас на україномовний форум з програмування, веб-дизайну, SEO та всього пов'язаного з інтернетом та комп'ютерами.
Будемо вдячні, якщо ви поділитись посиланням на Replace.org.ua на інших ресурсах.
Для того щоб створювати теми та надсилати повідомлення вам потрібно Зареєструватись.
Український форум програмістів → Алгоритми та структури даних, технології → Шлях на математичну вершину
Сторінки Попередня 1 … 26 27 28 29 30 … 41 Наступна
Для відправлення відповіді ви повинні увійти або зареєструватися
Ой яка краса!
1) А чим таке анімують?
2) А чи можна ще подивитися, як вектори «дихають»?
Хотів додати анімацію на wiki, але щось не вдається знайти відповідну формулу. Якщо знайдете, то киньте посилання і вкажіть точне місце.
Та хто його…
\cos \frac \sum разом зустрічаються в коді на 121 сторінці
Але далі ліньки ;-)
1) А чим таке анімують?
Wolfram Mathematica
2) А чи можна ще подивитися, як вектори «дихають»?
Що саме мається на увазі ? Намалюйте приблизну схему (статичну картинку), щоб я знав як то має виглядати.
ReAl написав:2) А чи можна ще подивитися, як вектори «дихають»?
Що саме мається на увазі ? Намалюйте приблизну схему (статичну картинку), щоб я знав як то має виглядати.
Мав на увазі вектори доданків суми, що утворюють вектор, який коли крутиться, то одна з його проекцій буде отой cos у лівій частині.
А тепер x=0, міняємо a, вектори доданків для цієї нульової фази якось «живуть».
Не такими сонними очима подивився на формулу, то тепер анімація буде цікава, але не обов'язкова :-)
Для n=2 два вектори доданків.
Зелене коло — одиничний радуіс, початки векторів доданків, звісно, в нулі, кінці рухаються по червоному колу діаметром
2/n = 1, між векторами π/2.
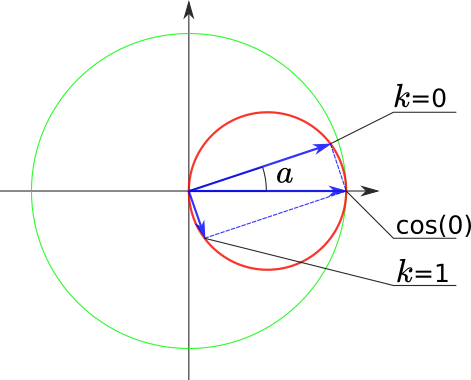
Для n=3 діаметр червоного кола буде 2/3 й відповідна кількість векторів.
Хотів додати сюди візуалізацію для формули (6), але wiki мені каже "Щось пішло не так" і дає дві кнопки "Спробувати ще раз" і "Приховати". Потрачено.
Залишу тут, може в когось получиться.
▼Прихований текст
Ідею зрозумів. Попробую щось таке зробити, але не знаю чи в мене получиться.
Ідею зрозумів. Попробую щось таке зробити, але не знаю чи в мене получиться.
Ідея в тому, що будь-які (ко)синусоїди — то вектори, що обертаються. З різними частотами-фазами. І зрозуміти, що (і чому) відбувається (і як на це вплинути), часом простіше по векторній діаграмі — «фото» цих векторів у якийсь момент часу з позначками/описом траєкторій.
це воно має виглядати, як юніт вектор, що використовує значення синусу чи косинусу в певній точці для обертання себе? Тобто. коли значенн 0 - то воно горизонтальне, а коли 1 - вертикальне вгору, а мінус 1 - вертикальне вниз?
це воно має виглядати, як юніт вектор, що використовує значення синусу чи косинусу в певній точці для обертання себе? Тобто. коли значенн 0 - то воно горизонтальне, а коли 1 - вертикальне вгору, а мінус 1 - вертикальне вниз?
куди? вліво? вправо?
FakiNyan написав:це воно має виглядати, як юніт вектор, що використовує значення синусу чи косинусу в певній точці для обертання себе? Тобто. коли значенн 0 - то воно горизонтальне, а коли 1 - вертикальне вгору, а мінус 1 - вертикальне вниз?
куди? вліво? вправо?
будемо брати знак останнього значення, що не дорівнює нулю. Якщо воно більше нуля, то вправо, а якщо менше, то вліво, наприклад.
це воно має виглядати, як юніт вектор, що використовує значення синусу чи косинусу в певній точці для обертання себе? Тобто. коли значенн 0 - то воно горизонтальне, а коли 1 - вертикальне вгору, а мінус 1 - вертикальне вниз?
У цьому конкретному прикладі одиничний вектор у результату cos(x) у лівій частині рівності, а інші вектори вже які будуть, їхні довжини взагалі змінні по косинусному закону.
Довжини векторів можуть бути пропорційні фізичним величинам, приклад такої векторної діаграми (і коли оті всі вектори закрутити з частотою 50 обертів на секунду, то їхні проекції на якусь одну вісь дадуть форми напруг, струмів, магнітних полів на різних частинах трансформатора).
такс, я зрозумів, це вони через це 
довели ось це 
та чо ви мені вподобайки ставите, але не допомагаєте???
ладно, озьдо, що я поки що вияснив...
Дивимось на жовте.
Коли ми розгортаємо квадрати, і перемножуємо те, що маємо, у нас виходить те, що зелене, та шлак у вишляді того, що синє. При цьому, якщо ми подивимось на зелене, то побачимо, що воно є субою добутків компонентів a та b, але не всіх компонентів, а лише тих, індекс котрих різний. Тобто, якщо а та b містять компоненти x, y та z, то ми бачимо добутки ax з by та з z, але не бачимо добутків компонентів з одним й тим самим індексом, тобто, не бачимо ax помножене на bx.
Коли би додаємо ці добутки, що представлені виразом помаранчевого кольору, то в нас є перемноження кожної компоненти вектору a, з кожною компонентою вектора b, а ми це можемо спростити до виразу, що виділений червоним кольором.
Тобто. спочатку ми додаємо помаранчеве до зеленого, і отримуємо червоне. Саме помаранчеве, це скалярний добуток двох векторів, і ми можемо записати його, як (a*b). І так, як ми додали помаранчеве до зеленого на початку, то в кінці (після перетворення їх суми в червоне), ми віднімаємо побаранчеве, котре записане, як сіре.
В кінці ми бачимо a2b2 - (a*b)2. З (a*b)2 все зрозуміло, це скалярний добуток. А от a2b2 - це вже перемножені вектори. Тобто, a - це ax+ay+az (і це все в квадраті), і для b - все так само.
Я все правильно розумію? Якщо так, то скажіть мені, будь ласка, куди поділось те, що виділене синім?
в мене тут думка з'явилась, а що, якщо ми не будемо перемножувати те, що виділене жовтим, а просто розкриємо дужки?
Спочатку я подумав, що у нас же там є від'ємні доданки, тобто, (a-b)2 розкладається в a2-b2. Але ж -b2 в результаті дасть нам додатнє число.. Чи може таке бути, що при розкритті дужок мінуси заміняються на плюси? Це б пояснило зникнення того, що виділене синеньким.
висновок ваш виглядає правильниним
стосовно синього рівняння, продовжу з моменту коли ми розклали жовте на
зелене - синєтепер додамо до нашого ріняння таку конструкцію яка ніяким чином його не змінить
зелене - синє + оранжеве - оранжевепогрупуємо їх
(зелене + оранжеве) - (синє + оранжеве)і тепер відповідно перша група перетворилась на червоне, а друга - на сіре
можете це перевірити вручну розкривши квадрат сірого рівняння
Спочатку я подумав, що там є відʼємні доданки, тобто (a−b)2 розкладається в a2−b2.
Але ж наче так
(a−b)2 = a2−2ab+b2
в мене тут думка з'явилась, а що, якщо ми не будемо перемножувати те, що виділене жовтим, а просто розкриємо дужки?
про яке перемноження ви говорите? зелене і синє рівняння якраз є наслідком розкриття дужок жовтого і зведення подібних доданків
та забийте на то, краще гляньте сюди
я думав, що ми можемо перетворити помаранчеве в сіре з використанням якихось параметрів квадратів, але виглядає так, що жовте і синж - то різні штуки.
На картинці я зробив розкладення для сірого, а думав, хоча на початку там помаранчеве.
Але я зара зрозумів, що це я зробив потрібне перетворення, але навпаки.
Ну, що ж. Тепер мені зрозуміло, звідки то все взялось. Буду читати далі, всім дякую, поки що можете бути вільними.
FakiNän написав:Спочатку я подумав, що там є відʼємні доданки, тобто (a−b)2 розкладається в a2−b2.
Але ж наче так
(a−b)2 = a2−2ab+b2
вподобайки ставимо, тому що ще не доросли самі до таких висот
(a−b)2 = (a−b) * (a−b) = a2 − ab − ba + b2 = a2 − 2*ab + b2
ви то для себе розписуєте?
я вище сказав, що думав, що (a-b)2 === a2-b2