Тема: Python в наукових дослідженнях
Хотів би започаткувати тут рубрику про застосування програмування на Python для вирішення наукових задач. Disclaimer: для багатьох пітоністів, як і для багатьох людей, пов'язаних таким чи іншим чином з науковою роботою, дані пости можуть бути очевидними. Але можливо для когось це буде цікавим матеріалом.
Передісторія. Я вчуся в аспірантурі на спеціальності "Автоматизація процесів керування". Об'єкт дослідження доволі вузькоспеціалізований, але він не має значення. Предмет дослідження ж - ідентифікація технічних станів промислових об'єктів. Пройшло перші півроку, і зараз я активно працюю в напрямі дата-майнінгу - застосуванням різних методів обробки до наявних даних з метою отримання додаткової, неочевидної на перший погляд інформації. Це виявлення прихованих періодичностей, трендів тощо. В даний момент мене зацікавив розклад часових рядів технологічних параметрів (допустимо, температури вузла, або вібраційної швидкості підшипника) в нетривіальні базиси. Зазвичай розклад відбувається по функціях Фур’є, але є інші базиси, простіші для обробки комп’ютерами: функції Радемахера, Хаара, Крестенсона, Уолша. І дають вони доволі цікаві результати. Однак, невідомо, чи це буде цікаво середньостатистичному читачу цього форуму. Є тема ближча - алгоритми стискання.
Маленька теоретична підготовка
Коли я рився в інтернеті в пошуках інформації про функції Хаара, натрапив на цікаву статтю на одному відомому російському ресурсі. Там функція (або вейвлет) Хаара застосовувалася для стистення зображень. Сама функція виглядає дуже просто:
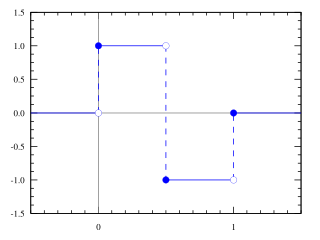
Як же стискалося зображення? Просто, як двері: для чорно-білого фото бралися значення сусідніх пікселів і в один масив записувалася їх півсума, а в другий їх піврізниця. І так для кожної пари пікселів. А потім масив піврізниць просто відсікався. Таким чином, ми отримували масив удвічі меншого розміру з усередненими значеннями для кожної пари пікселів. Повторюся, все дуже просто.
А тепер найцікавіше: а як же втрати? Втрати для кожного конкретного випадку будуть дуже різними. Допустимо у нас є зображення, подібне до шахової дошки - білий піксель-чорний піксель і т.д. Після першого такого стискання у нас вийде повністю сіре зображення. Зміст повністю втратиться, чого нам дуже не хотілося б.
На щастя, реальні фотографії характерні тим, що сусідні пікселі мають дуже близькі значення. І до них цей метод стиснення застосовується доволі ефективно.
Ми зациклилися на зображеннях. В даному випадку чорно-білі зображення - це всього лиш масиви значень відтінку сірого для кожного пікселя. Довгий час працюючи з технологічними параметрами мого об'єкта дослідження, я приблизно вивчив їх характер змін у часі. Специфіка така - з кожного давача значення знімається кожних 5 хвилин. І, так вже сталося, що дані технологічні об’єкти майже не мають змін у параметрах функціонування з коротким періодом - сусідні значення у більшості випадків рівні, або майже рівні. Тому я вирішив просто для себе провести
Стискання масиву часового ряду одного параметра з допомогою вейвлета Хаара
Скільки тексту прийшлося написати, щоби нарешті дістатися до коду=) Підключав я для цього дві бібліотеки - scipy.io (для завантаження даних з файлу .mat, в якому вони зберігалися по замовчуванню) та pylab (для перегляду проміжних резутьтатів).
Функція load (для завантаження даних):
def load():
data = scipy.io.loadmat('data0.mat')
mdata=data['data0']
return mdataФункція compress (для стискання цих даних):
def compress(mdata):
a=[]
b=[]
isEven=[]
for e in mdata:
b.append(e)
if len(mdata)%2==0:
isEven.append(True)
else:
b.append(mdata[len(mdata)-1])
isEven.append(False)
for e in range(int(len(b)/2)):
a.append((b[e*2]+b[e*2+1])/2)
return aВ принципі, пояснювати тут нічого. Єдине - масив isEven я думав застосовувати в перспективі, поки що обходиться без нього. Відповідно, приведу тут же функцію decompress:
def decompress(a):
rdata=[]
for e in a:
rdata.append(e)
rdata.append(e)
return rdataВсе просто - вона дублює значення зі стиснутого масиву. Що ж у нас вийшло в резутьтаті? Ось вихідні дані:
[img]http://i47.домен агресора/big/2013/0622/0f/c28d03192936fe8833e277c7f0b1d10f.png[/img]
А ось відновлені:
[img]http://i48.домен агресора/big/2013/0622/e4/fcded02c8c909aac99594252680e11e4.png[/img]
Ви бачите різницю? Я ні. І це при стисненні в 2 рази! Однак, людське око - штука непевна. Давайте подивимося, що скаже нам про ці дані комп’ютер. Для порівняння вихідних та відновлених даних була написана функція compare:
def compare(mdata,rdata):
i=0
mmean=sum(mdata)/len(mdata)
rmean=sum(rdata)/len(rdata)
s1=0
s2=0
s3=0
for e in range(len(mdata)):
s1+=(mdata[e]-mmean)*(mdata[e]-mmean)
s2+=(rdata[e]-rmean)*(rdata[e]-rmean)
s3+=(rdata[e]-rmean)*(mdata[e]-mmean)
r=s3/((s1*s2)**0.5)
print r
for e in range(len(mdata)):
if mdata[e]==rdata[e]:
i=i+1
print float(i)/len(mdata)Функція ця виводить два значення. Спочатку про друге - цілком логічна штука - відношення співпадінь значень у відновлених і вихідних даних до загальної кількості даних. Однак математики користуються іншим критерієм - коефіцієнтом лінійної кореляції (студенти, які вчили теорію ймовірності і матстатистику, мали б бути знайомі з цим поняттям). Його формула дуже проста, вона є у Вікіпедії, не буду переписувати інформацію звідти. Власне змінна r якраз і є цим коефіцієнтом.
Які ж вони результати дають нам при стисненні в два рази?
Коефіцієнт лінійної кореляції: 0.99426435
Кількість значень, що співпали: 0.959474885845
Погодьтеся, не найбільші втрати при такому стисненні. Кореляція в 99,4% - це взагалі прекрасний результат.
Ви можете сказати: окей, чувак, ти взяв такий відрізок з однієї з функцій і воно так красиво працює. Що з іншими? Проведемо ці самі операції стиснення з 5 різними параметрами - серед них є і температура, і тиск, і віброшвидкість. Більше того, додамо результати для стиснення в 4 та 8 раз, провівши стиснення та відновлення 2 та 3 рази відповідно. Що ми отримуємо? Ідентичність значень:
[img]http://i47.домен агресора/big/2013/0622/16/ace1da60e1af4399497d057c7530b816.jpg[/img]
Коефіцієнт кореляції для цих значень:
[img]http://i46.домен агресора/big/2013/0622/48/7aa254097eebc0449ee69c2e9fde5d48.jpg[/img]
Можете побачити, як відновлення залежить від характеру даних. Тому, якщо оформляти цей алгоритм "по-дорослому", хорошим рішенням буде його проектування з деякою мірою адаптивності відносно вихідних даних. Тим не менше, відновлена функція після стиснення у 8 разів корелює з вихідними даними на 96-99%.
Я думаю, що проведені операції дають можливість зробити логічний
Висновок:
даний метод стискання до даних такого характеру можна ефективно застосовувати, більше того, він може бути елементом більш вдосконаленого алгоритму стискання, що прекрасно працюватиме з подібними даними, сусідні значення яких дуже подібні.
P.S. Власне я продовжив розвивати тему удосконалення цього алгоритму, і в мене дещо вийшло. Якщо вам буде цікаво, із задоволенням поділюся=)

