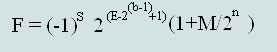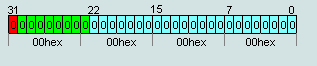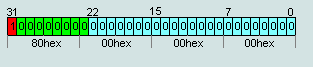Тема: Дробові числа. Частина 1
Щось сьогодні з'явилось бажання написати про комп'ютерне представлення дробових чисел, а точніше числа з плавучою комою.
Напевно тут всі знають що зараз в 99.9% процесорів і мікроконтролерів зберігають такі числа згідно стандарту IEEE 754. Перша версія стандарту була випущена в далекому 1985 р. і визначала 4 основних типи: числа одинарної точності, подвійної точності, розширене число одинарної точності (використовується дуже і дуже рідко) і розширені подвійної точності.
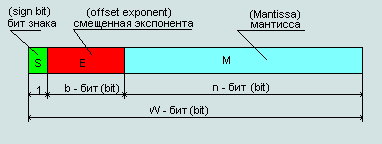
Вони використовують 32, 64, >43 і >79 біти відповідно.
Для різних чисел розмір E І M є різним зокрема:
Для чисел одинарної точності: E = 8 біт M = 23;
Для чисел подвійної точності: E = 11 біт M = 52;
Для чисел розширеної одинарної точності: E = ≤11 біт M = решта;
Для чисел розширеної одинарної точності: E = 15 біт M = решта;
Перетворення виконується за наступним алгоритмом:
1. Перетворити в двійкову систему число.
2. Привести число до нормалізованого вигляду (це коли мантиса в межах від 1 до основи системи, тобто в даному випадку 2) ,для малих можна і до ненормалізованого).
3. Визначити зміщену експоненту*.
*Для того щоб не вводити ще один біт знаку для експоненти її просто зміщують на 2^(n-1)-1, де n - кількість біт на експоненту.
Для прикладу число 12,25 буде виглядати так:
1. 12,25d = 1100,01b
2. 1100,01b = 1,10001b * exp^(11b)
3. E = 127d + 3d = 130d = 10000010b
Тобто це число буде виглядати так :
0100 0001 0100 0100 0000 0000 0000 0000 = 0x41440000
До речі, забув сказити, в мантису записуються тільки числа після коми.
Перетворити назад можна за формулою:
, де E - значення експоненти,
b - кількість біт на експоненту
n - кількість біт на мантису
Але тут виникає кілька проблем, зокрема неможливо зобразити нуль. Тому для деяких чисел були введені спеціальні значення зокрема
Також для більш малі числа можна зберігати в денормалізованій формі. Для цього в експоненті мають бути всі нулі
P.S. Вибачте за можливі помилки і можливо неправильні деякі терміни.
P.P.S В другій частині напишу про проблеми такого представлення.