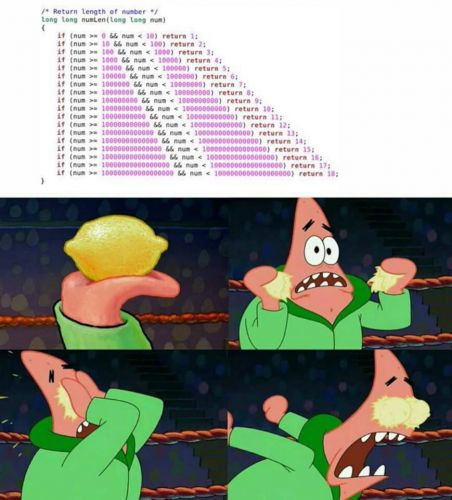
Наштовхнувся в мережі на ось таку творчість:
Автор картинки, вочевидь, вважає цей код поганим. Серед претензій в коментарях я побачив таке:
- код довгий;
- код надмірний (немає циклу, зайві умови, немає else);
- код не використовує стандартні функції, якими тут можна було б скористатися.
Ну що ж, розберімося. Для початку: довжина коду (в межах розумного, звісно) не має особливого значення, значення має читаність, і тут вона непогана: мета чітко зрозуміла, як вносити зміни (наприклад, якщо знадобиться від'ємні числа враховувати) - теж видно. Єдине, що можна було б краще код вирівняти, щоб другий стовпчик чисел був по одній вертикалі, це допомагає краще бачити помилки; порівняння в таких випадках краще розташовувати у вигляді
(1000 <= num && num <10000)
це робить очевидним, що перевіряється належність числа інтервалу; і return краще виносити на наступний рядок, але в цьому коді, гадаю, краще саме так. Ну добре, але ж можна було зробити й коротший код читаним? Так, звісно. Читаність — не перевага цього коду, але й не недолік.
Відсутність else? Ні, тут це не має значення: якщо якась умова виконається, то відбудеться return, і подальший код не буде виконуватися в будь-якому разі.
Зайві умови? Так, є трохи. Справді, після перевірки на num<10 немає сенсу перевіряти, чи виконується n>=10 (виконується), тому перші половини всіх умов можна просто викинути. Сучасні компілятори часто бувають достатньо просунутими, щоб зрозуміти можливість цієї оптимізації, а перевірка - дуже швидка операція, тому в результаті швидкість виконання від цього майже не страждає; але нащо ж змушувати компілятор з процесором перепрацьовувати?
Але ж це все можна було загнати в цикл чи скористатися стандартними функціями? Так. Але цей код має несподівану перевагу: він в біса швидкий. Я зібрав десяток інших способів пошуку довжини числа; цей код посідає 3-є місце серед них за швидкістю, а з оптимізацією - ділить 2-е з ним же без зайвих умов. Використовувався clang 7.0.0 з -o3.
▼Код
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <sstream>
#include <cmath>
#include <random>
#include <limits>
#include <array>
#include <chrono>
/*****************************************************************
* number length
* naive optimization
******************************************************************/
long long num_len1(long long num)
{
if( 0<=num && num< 10 ) return 1;
if( 10<=num && num< 100 ) return 2;
if( 100<=num && num< 1'000 ) return 3;
if( 1'000<=num && num< 10'000 ) return 4;
if( 10'000<=num && num< 100'000 ) return 5;
if( 100'000<=num && num< 1'000'000 ) return 6;
if( 1'000'000<=num && num< 10'000'000 ) return 7;
if( 10'000'000<=num && num< 100'000'000 ) return 8;
if( 100'000'000<=num && num< 1'000'000'000 ) return 9;
if( 1'000'000'000<=num && num< 10'000'000'000 ) return 10;
if( 10'000'000'000<=num && num< 100'000'000'000 ) return 11;
if( 100'000'000'000<=num && num< 1'000'000'000'000 ) return 12;
if( 1'000'000'000'000<=num && num< 10'000'000'000'000 ) return 13;
if( 10'000'000'000'000<=num && num< 100'000'000'000'000 ) return 14;
if( 100'000'000'000'000<=num && num< 1'000'000'000'000'000 ) return 15;
if( 1'000'000'000'000'000<=num && num< 10'000'000'000'000'000 ) return 16;
if( 10'000'000'000'000'000<=num && num< 100'000'000'000'000'000 ) return 17;
if( 100'000'000'000'000'000<=num && num<1'000'000'000'000'000'000 ) return 18;
return 0;
}
/*****************************************************************
* number length
* to string c-style
******************************************************************/
long long num_len2(long long num)
{
char s[21];
std::sprintf(s,"%lld",num);
return strlen(s);
}
/*****************************************************************
* number length
* to string c++-style
******************************************************************/
long long num_len3(long long num)
{
std::stringstream s;
s<<num;
return s.str().length();
}
/*****************************************************************
* number length
* loop - division
******************************************************************/
long long num_len4(long long num)
{
if(num==0)
return 1;
long long length = 0;
while(num>0) {
++length;
num/=10;
}
return length;
}
/*****************************************************************
* number length
* no lower checks
******************************************************************/
long long num_len5(long long num)
{
if( num< 10 ) return 1;
if( num< 100 ) return 2;
if( num< 1'000 ) return 3;
if( num< 10'000 ) return 4;
if( num< 100'000 ) return 5;
if( num< 1'000'000 ) return 6;
if( num< 10'000'000 ) return 7;
if( num< 100'000'000 ) return 8;
if( num< 1'000'000'000 ) return 9;
if( num< 10'000'000'000 ) return 10;
if( num< 100'000'000'000 ) return 11;
if( num< 1'000'000'000'000 ) return 12;
if( num< 10'000'000'000'000 ) return 13;
if( num< 100'000'000'000'000 ) return 14;
if( num< 1'000'000'000'000'000 ) return 15;
if( num< 10'000'000'000'000'000 ) return 16;
if( num< 100'000'000'000'000'000 ) return 17;
if( num<1'000'000'000'000'000'000 ) return 18;
return 0;
}
/*****************************************************************
* number length
* loop - multiplication
******************************************************************/
long long num_len6(long long num)
{
if(num==0)
return 0;
long long power = 10;
for(long long length=1; length<19; ++length) {
if( num<power ) return length;
power *= 10;
}
return 0;
}
/*****************************************************************
* number length
* loop - power
******************************************************************/
long long num_len7(long long num)
{
if(num==0)
return 0;
for(long long length=1; length<19; ++length)
if( num<pow(10,length) ) return length;
return 0;
}
/*****************************************************************
* number length
* logarithm
******************************************************************/
long long num_len8(long long num)
{
if(num==0)
return 1;
return log10(static_cast<long double>(num))+1;
}
/*****************************************************************
* number length
* recursion - division
******************************************************************/
long long num_len9(long long num)
{
if(num<10)
return 1;
return num_len9(num/10)+1;
}
/*****************************************************************
* number length
* tail recursion - multiplication
******************************************************************/
long long num_len10(long long num, long long length=0, long long power = 10)
{
if(length>18)
return 18;
if(num<power)
return length+1;
return num_len10(num, length+1, power*10);
}
/*****************************************************************
* number length
* dichotomy
******************************************************************/
long long num_len11(long long num)
{
if(num<1000000000) {
if(num<100000)
{
if(num<1000){
if(num<100)
{
if(num<10)
return 1;
else
return 2;
} else { //>=1e2
return 3;
}
} else { //>=1e3
if(num<10000)
return 4;
else
return 5;
}
} else { //>=1e5
if(num<10000000){
if(num<1000000)
return 6;
else
return 7;
} else { //>=1e7
if(num<100000000)
return 8;
else
return 9;
}
}
} else { //>=1e9
if(num<100000000000000){
if(num<1000000000000){
if(num<100000000000) {
if(num<10000000000)
return 10;
else
return 11;
} else { //>=1e11
return 12;
}
}else{ //>=1e2
if(num<10000000000000)
return 13;
else
return 14;
}
} else { //>>1e14
if(num<10000000000000000)
{
if(num<1000000000000000)
return 15;
else
return 16;
} else { //>=1e16
if(num<100000000000000000)
return 17;
else
return 18;
}
}
}
}
void test_eq(long long a,long long b, const char *msg, long long data)
{
if(a!=b){
std::cout<<a<<" should equal "<<b<<"! "<<msg<<" of "<<data<<"\n";
abort();
}
}
int main() {
std::default_random_engine generator;
std::uniform_int_distribution<long long> distribution(0,100000000000000000);
for(int i=0; i<1000; ++i)
{
long long rnd = distribution(generator);
long long v1 = num_len1(rnd);
long long v2 = num_len2(rnd);
long long v3 = num_len3(rnd);
long long v4 = num_len4(rnd);
long long v5 = num_len5(rnd);
long long v6 = num_len6(rnd);
long long v7 = num_len7(rnd);
long long v8 = num_len8(rnd);
long long v9 = num_len9(rnd);
long long v10 = num_len10(rnd);
long long v11 = num_len11(rnd);
test_eq(v1, v2, "v2", rnd);
test_eq(v1, v3, "v3", rnd);
test_eq(v1, v4, "v4", rnd);
test_eq(v1, v5, "v5", rnd);
test_eq(v1, v6, "v6", rnd);
test_eq(v1, v7, "v7", rnd);
test_eq(v1, v8, "v8", rnd);
test_eq(v1, v9, "v9", rnd);
test_eq(v1, v10, "v10", rnd);
test_eq(v1, v11, "v11", rnd);
}
std::cout<<"Test done!\n";
std::array<long long, 1000000> data;
for(auto &x:data)
x = distribution(generator);
#define BENCHMARK(function) \
{ \
long long s = 0; \
auto start = std::chrono::high_resolution_clock::now(); \
for(auto x:data) \
s += function(x); \
auto end = std::chrono::high_resolution_clock::now(); \
double time_lapse=std::chrono::duration_cast<std::chrono::duration<double>>(end - start).count(); \
std::cout<<#function<<": "<<s<<" in "<<time_lapse<< " seconds\n"; \
}
BENCHMARK(num_len1)
BENCHMARK(num_len2)
BENCHMARK(num_len3)
BENCHMARK(num_len4)
BENCHMARK(num_len5)
BENCHMARK(num_len6)
BENCHMARK(num_len7)
BENCHMARK(num_len8)
BENCHMARK(num_len9)
BENCHMARK(num_len10)
BENCHMARK(num_len11)
}
Місця з кінця, час на мільйон операцій на сервері repl.it. Час я трохи округлив.
11. 3.6с. №7. Наївний цикл, з обчисленням 10**i в кожній ітерації. Піднесення до степеня - дуже повільна операція.
10. 2.8с. №3. Перетворюємо число в стрічку за допомогою об'єктів. Це - приблизний аналог Python-івського len(str(num)). Дуже повільно, бо всі тимчасові об'єкти виділяться-знищуються.
8-9. 0.8с. №4, №9. Цикл і рекурсія з діленням. Ділення - повільна операція.
6-7. 0.4с. №2. Перетворення в стрічку за допомогою sprintf.
№10. Хвостова рекурсія з множенням; загалом мала б бути швидшою, можливо, clang чомусь не тягне, треба розбиратися.
5. 0.16с. №6. Цикл з множенням.
4. 0.14с. №8. Логарифм. Логарифм - теж не швидка операція, але поза циклом не так вже й погано.
2-3. 0.03с. №1. Очікувано наша функція.
№5. Вона ж, але без зайвих умов. Оптимізація зрівнює ці дві функції за швидкістю.
1. 0.02с. №11. Приблизно те саме, але тепер порівняння відсортовані так, щоб кількість порівнянь була приблизно однаковою, за принципом бісекції.
Таким чином, ми бачимо, що позірно надмірний код може бути, насправді, просто оптимізованим. Не поспішайте робити висновки, коли бачите незрозумілий код - спробуйте уявити собі, що думав програміст, коли писав це. Особливо якщо код явно дбайливо вирівняний.