От сьогодні я був задумався над теоремою Піхвагора.
Воно каже - сума квадратів катетів дорівнює квадрату гіпотенузи. І тут я був захтів розібратись - як той Піф дійшов до цього висновку? Як, взагалі, люди придумують оті всі круті формули, котрі реально працюють?

Я почам роздумувати над отою формулою, і в вуха відразу вдарилось слово - "квадрат". Що це взагалі таке? Раніше, квадрад для мене значив те, що число ділиться саме на себе, і в верхньому правому кутку, біля числа, записується маленька двійка. Але чому саме квадрат? Чому не трикутник?

І тут я пойняв - квадрат числа, то є площа квадрату, сторона котрого дорівнює числу.
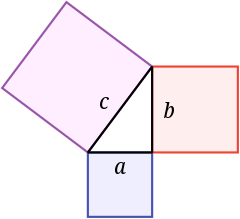
От я вам картинку намалював.

Нехай ми маємо трикутник, перший катет має довжину сторони 3, а другий 4.
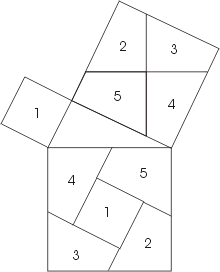
Формула нам каже, що нам потрібно взяти два квадрати, сторони котрих 3 і 4 сантиметри, і додати їх. Після цього ми отримаємо площу квадрата, в котрий могли б поміститись два перших квадрати, якщо їх порізати на шматочки і позапихати туди. І ось сторона цього нового квадрату і буде нашою гіпотенузою.

От не знаю, як то міг зрозуміти Піф, як тільки не спостерігаючи за квадратиками. Я то і на картинці намалював, ота напівпрозора штука - перевернутий квадрат з площею, котра дорівнює площам менших квадратів, зі сторонами 3 і 4.

Ще я помітив закономірність між квадратами чисел. Різниця між кожною наступною парою квадратів збільшується на два. Таким чином різниця між 9 і 16 буде 7, а між 16 і 25 = 9, і так далі. А ще я помітив, що ця різниця дорівнює сумі чисел чи цифр без квадрату. Адже 9 - це квадрат 3, а 16 квадрат 4, і різниця між квадратами == 7, а сума неквадратів теж сім, адже 4+3. І з 16 і 25 так само, різниця 9, а сума 4+5, теж 9.
Можливо, це можна використати при якійсь хардкорній оптимізації.

Наприклад, нам треба вивести квадрати кожної цифри від 4 до 10, то навіщо нам рахувати квадрати для кожної циферки, якщо ми можемо спершу обрахувати квадрат першого числа, а потім просто додавати до нього суму поточного і наступного числа.

int firstSqr=4*4;
for(int i = 4; i<10; i++)
{
print(firstSqr);
firstSqr+=(i+i+1);
}

Він розглядав не трикутник, а квадрати, які у суміші утворюють трикутник, якщо їх вершини стикаються з вершинами сумісного квадрату. Отож якщо квадрат обчислюється плошиной, то його сторона - корнем плошини. Звідтіля й формула де використовуються саме квадрати:

Так написано у Вікі, а вигадано саме історичними подіями )

то такий футбольор?

дуже важка картинка!

не пойняв

мабуть, тому, що ви думаєте евклідовою геометрією (якою навчають в школі), а треба Лобачевською

Суспільна обструкція, зрештою звільнення. І не квантова фізика, а теорія відносності будується на узагальнені геометрії Лобачевського - просторі Мінковського.

Якщо не ставити перед собою амбітних завдань, то і результат буде не дуже.